linear regression

Introduction to linear regression:

Linear regression is the first prediction algorithm taught in statistics to the students who begin their journey in the line of prediction and prescribing and doing all sorts of statistics wizardry. Being a statistics student, in this post, I will provide a introduction to linear regression for people not so into maths and go into bit by bit into the details, use of linear regression in different statistical packages and therefore try to balance it out for people looking at linear regression from statistics point of view by helping them into getting the application side.

In this post, we will discuss about the following topics:

1. what is linear regression
2. different types of linear regression
3. What are the applications of  linear regressions?
4. How to interpret results of linear regressions?
5. adjusted R-square and mean-squared-error
6. coefficients and their significance
7. Assumptions of linear regression
8. assumption of multivariate-normality
9. what is homoskedascity
10. assumption of independence of the predictor variables
11. assumption of no autocorrelation
12. analytical and theoretical solution of a linear regression
13. verification of assumptions in linear regression
14. how to check multicollinearity
15. How to implement linear regression

What is linear regression?

Linear regression is one of the most basic predictive process. As the name suggests, linear regression is used to find out linear relation between dependent variable and an independent variable. If you don't know, in a prediction, dependent variable means the variable which is considered to be dependent on other factors and independent variable refers to the mutually independent variables which effect the value of the target variables. In case of linear regression, the relation between dependent and independent variables are assumed to be linear.
In general, a perfectly linear relation is generally hard to expect. But surprisingly enough, a linear model, being basic enough though, behaves pretty well to predict and explain the effects of different independent variables on a target/dependent variable.

different types of linear regression:

Largely, there are two different types of linear regression. First one is simple linear regression while the other one is multivariate linear regression. 

A simple linear regression is a linear regression where a dependent variable Y is linearly dependent on dependent variable X. In this case, the formula is expressed as:

Y = c+ bX

where X is independent variable, Y is dependent variable, c is a constant, b is the co-efficient of the variable X. 

A multi-variate linear regression is a linear regression where a dependent variable Y is linearly dependent on multiple variables X1, X2, ..., Xn. In this case, the formula of a regression is expressed as:

$Y=c_0+c_1{X}_1+c_2{X}_2+...+c_{\mathrm{n}}{X}_{\mathrm{n}}$

In this case,$\mathrm{Y}$ is the dependent variable, and ${\mathrm{c}}_0$ is the constant, ${\mathrm{c}}_{\mathrm{i}}$ are coefficients for the variables; ${\mathrm{X}}_{\mathrm{i}}$ are the dependent variables.

What are the applications of  linear regressions?

Linear regression is used mainly to predict

(1) the effects of the independent variables on the dependent variable

(2) the prediction of the target variables

Linear regression can be solved analytically, and therefore, we produce statistical significance of the independent variables using those methods, and thus we can talk about the effects with proper statistical terms and measured risk and confidences. This gives linear regression method an edge over many of the computer science algorithms which often suffer from the problems of explanability  as for how a dependent variable changes and/or get influenced due to a independent variable.  In such cases, linear regression is extremely useful because of its simple and statistics backed structure. 

Nowadays, linear regression is not the best option to predict a numeric variable as a dependent variable of a group of independent variables, but yes, often, when one needs to both explain as well as predict in details, linear regression is used to predict target variable too. We will explore how to predict target variable using linear regression in details in later sections of this post.  

How to interpret results of linear regressions?

This is one important part when it comes to use a result of linear regressions. Often, people in business positions have to use results of linear regressions, but that comes not as a easy job. Two main parts of a linear regressions are important and should be noted and used. The parts are:

(1) adjusted R-square and mean-squared-error:

 In a linear regression, the R-square is the measure of accuracy of the linear regression. The R-square can be from 0 to 1 i.e. it can also be interpreted as from 0 to 100%. Roughly speaking, R-square denotes the amount of variance in the data which is described by the linear regression. The more amount of variance gets described by the linear regression, the better the regression is. So, to describe how efficient a linear model fitting has been, one can depend on how high the adjusted R-square percentage is. 

While adjusted R-square is an accuracy from the statistical point of view, the more application point of view is the mean-squared-error (mse). Mean-squared-error is the mean of the squares of the errors in prediction using the linear model over training data. A small mse means that when the linear regression is used, the error in prediction which happens, is going to be near root of mse i.e. rmse. So, the smaller mse directly presents a smaller error in prediction.

(2) coefficients and their significance:

In a linear regression, the coefficients of a independent variable denotes the effect of the independent variable on the dependent variable. i.e. consider that in a regression problem, the coefficient of X is 0.2, which in simple terms denote that on 1 increment of X, Y will increase by 0.2. While this is roughly correct, assumptions of independence of the independent variables are not often strongly held in practical applications, but we will come to that later. Also, sometimes, we try to see whether coefficients are significant statistically. In that case, we run a linear regression and check the p-value of the coefficients. If p-values are higher than 0.05, then one can say that the corresponding coefficients are not significant. Although it may sound a bit hard at this section, be with me as we will explain the reasoning in later section in details.

Once you understand the statistical background in details, you will be able to interpret it in several other ways. Now, let's head into the first steps of solving a linear regression problem.

Assumptions of linear regression:

To solve a linear regression system, we assume a lot of things. We will discuss the assumptions made to solve general linear regression, i.e. multivariate linear regression.
The equation of multivariate linear regression is:

$Y=$β$X+$ε
where $$β is a vector of co-efficients of the variables, X is the design matrix and $$ε is a vector of errors.

Here, design matrix is the matrix where each row represents one data point with the values of each variable and each column represents the values of each variable across all the data points.
Now, let us dive into the assumptions:

(1) assumption of multivariate-normality:

the errors are assumed to be identical and independently distributed to $N~(0,$σ²$)$
or in case of multivariate linear regression, it is assumed that,

ε ~ N(0, Σ)

Where:

• ε (epsilon) represents the error term.
• Σ (uppercase sigma) represents the correlation matrix of the errors.
• σ (lowercase sigma) represents the standard deviation.

This notation indicates that the error term ε follows a normal distribution N with a mean of 0 and a covariance matrix Σ.

(2) homoskedascity:

It is assumed that the σ is constant, i.e. it is independent of the size of the data, and does not change with the number of instances of data. This assumption, while may sound easy, doesn't hold right always. But more on that later.

(3) independence of the predictor variables:

the predictor variables are assumed to be independent of each other; i.e. none of them should have any correlation with each other. This translates in form of the equation that, if the size of X is (n,k), then the matrix is full column rank, (as in general n>k). 

(4) Linear relationship:

the easiest, but important assumption is that the target variable and each of the predictor variable is related in linear relationship. This is again kinda strong assumption. Many times, linear relationship doesn't hold, but for the most portion of the application part, a linear relationship works pretty fine. 

(5) No autocorrelation:

This assumption says that the residuals are not auto-correlated, i.e. the residuals at t , doesn't effect residuals at t+1. This can be checked by observing that whether the residuals are correlated to each other or not. 

There are some other small assumptions which are mere technicalities. But those are mostly not important. So,we will keep these assumptions in mind and proceed to see how it gets solved.

Analytical solution of Linear regression:

Solving the linear regression is quite a bit technical. Let's start with the problem equation again and what we want to solve. In the equation,

Here’s the transformed and rewritten version of your expression with symbols:

Y = βX + ε

Where:

• β (beta) are the unknown parameters we want to predict.
• ε (epsilon) is the error term.

To estimate the unknown parameter β, we want to minimize the norm of the errors. We aim to minimize the expression:

‖ ( Y - βX )ᵀ ( Y - βX ) ‖

To find the value of β that minimizes the norm, we take the derivative of the expression inside the norm with respect to β and set it equal to 0. After performing the derivation, we obtain:

β = (XᵀX)⁻¹ XᵀY

Where:

• Xᵀ is the transpose of matrix X.
• (XᵀX)⁻¹ is the inverse of the matrix XᵀX.
• Y is the observed data.

This is the ordinary least squares (OLS) solution for estimating β.

So, there it is, the theoretical solution of linear regression. Now, here are some technicalities which I am not going to further delve into. You can derive the standard deviations of β, i.e. the coefficients and then formulate the standard t-test for significance of the co-efficients. For further details, please follow this awesome stat-book.

How to use Linear regression

There are two parts of a linear regression use in practical cases. First one is the verification of the assumptions and the second one is the fitting of the dataset in a linear regression packages. We will first talk about how to do the checking of the assumptions.

verification of assumptions

assumptions of normality:

To check normality of the errors, one can run the linear regression, calculate the errors, and then check the errors for normality. For normality check, there are multiple tests, but you can use shapiro-wilk normality test.

assumptions of linear relationship:

To check linear relationship, you have to plot the target variable vs the predictor variable. The plot, if surrounds around a line, then it supports a linear relationship, while if it is scattered circularly, then it doesn't support linear relationship. This idea is also depicted by the pearson correlation of the predictor variable and target variables. In general, if the correlation is below $\mathrm{10}-3$, then there is no or little relation between the predictor and the target variable. One other way to check if there is any correlation is to create a random data sample, with a similar range to that of the predictor variable and then check its correlation and plots with the predictor variable. If it is similar to that of the target variable vs predictor variable then clearly the predictor variable doesn't have any significant variable and if the predictor variable has a significantly better correlation and linear plot with target variable then, it means there is some amount of correlation and linear relationship with between target and predictor variable.

multi-collinearity check and prevention:

what is multi-collinearity?

Often in a dataset, predictor variables are dependent and highly correlated with each other. This is called multi-collinearity. Often this is a doubt that how high the correlation should be to call two columns as highly collinear and it needs attention. For this, generally, you can consider 0.9 as a correlation, but if you are too restrictive then you can even consider correlations higher than 0.75 as highly correlated. More discussion on this can be followed here on stackoverflow.

how can we check multicollinearity?

There are quite several ways to check multicollinearity.
The first and most popular one way is to find out VIF. VIF is the variance inflation factor.VIF of a predictor variable is a measure of R-squared for the regression of the predictor variable being predicted by all the other predictor variables. So if VIF is high, it means that the corresponding variable can be predicted well by the other variables, therefore high multicollinearity is present. For a general rule of thumb, if VIF is greater than 10, definitely multi-collinearity is present, while a VIF 5-10 also suggests some amount of multicollinearity. One other similar term you may have heard about, which is tolerance. Tolerance is the inverse of vif, and just from what we discussed above, a tolerance less than 0.1 denotes high multi-collinearity.

There are certainly other ways to find multi-collinearity. To start with the procedures, one can start checking correlations between pairs of the predictor variables and then if you find high correlations, then that is a sign of multicollinearity.
Also, you can check standard deviations of the predictor variables. The high variance of the predictor variables often denotes that some of the predictor variables have high collinearity and therefore the estimates are not accurate enough to have low variances.
Other than that, you can consider business points of view for the coefficients. Often from the business or context of the linear regression, you will have an idea about which variables should have high coefficients of variables and which variables should influence the target variable in which direction. But generally, the coefficients will not have the proper sizes, or will not show the proper signs in general when collinearity shows up. These are concepts that are not direct ways to analyze but ways to realize or detect multicollinearity once you have run your regression already.
There are other ways to find out multicollinearity, as such condition index, but these are way less obvious and direct than the ways I have mentioned already.

The main way to prevent or vanish multicollinearity, the normal way is to avoid taking one of the rows which creates multicollinearity. Generally, we consider which variable has more explainability or coefficient on the linear regression and then delete the other variable which is highly correlated. There are some other ways, i.e. RFE method which deletes the weakest columns at each step, or increasing variables method, which generally adds one or number of variables and looks at improvement of the performance of prediction. If the improvement is not significant then we often know that the variables are not sufficiently significant. In this way, we eliminate the variables which don't improve the performance.

How to solve non-normality?

The other problems, i.e. non-normality and homoskedasticity can also be solved sometimes using probabilistic methods. Beta distributions, chi-square distributions, and many other distributions can be transformed into normal distributions using specific transformations. Therefore, whenever errors do not satisfy the normality, one can transform the error vector in a way to fit it into normality and therefore apply the linear transformation solution.

How to solve non-linear relationship problem between predictor and target variable?

Also, when there is evidence of a lack of linear relationship between a predictor variable and a target variable, but they are correlated, then one can look at the corresponding graph.These graphs let us know that often the target variables are polynomially or logarithmically connected with the predictor variable. In these cases, we can use the polynomials or log of that predictor variable as a new variable instead of that predictor variable as that transformation is in linear relation with the target variable. This is the way one remedies the problem of not having a linear relationship between the predictor and the target variable. If even after transformation there is not much correlation, then one should not use that predictor variable anyway.

How to implement linear regression:

There is a number of statistical languages to use linear regression on. We will discuss how to use linear regression on R, Python, Julia, and several other languages. Please read through this section as this is the most applied section as you can use similar codes whenever you need to use linear regression in practical cases.

Linear regression using python:

There are two packages in python to use linear regression. One of them is statsmodels.api where the other one is sklearn.linear_model. First I will discuss what is the difference between these two and when you should use which one. The statsmodels package is one that gives the statistical significance of the features used in regression and therefore, statsmodels are important when you run a linear regression for sake of feature importance analysis, t-test of features and verify other statistical significances. But as it not only solves the linear regression parameter optimization but also runs all these tests, checks significances and other things, therefore, this package is significantly slower than the sklearn package when you run the regression on a moderate amount of data, i.e. million rows and so on. Therefore, when you want more of a prediction sort of work to be done by the regression, and don't want to focus on the statistical tests or significances, then sklearn is clearly a better choice to go with, as it will be fast and easier to implement.

Also other than clarifying this point, I will want to clarify one more difference between sklearn and statsmodels. sklearn fits the linear regression by default with an intercept variable i.e. a column of 1 is taken as a predictor variable which is analogous to the intercept in case of a simple 2-dimensional linear regression. But by default, the statsmodel doesn't fit an intercept variable. That's why, whenever you want to take an intercept variable which you should always; if not specified otherwise by some specific theory, then you have to manually add that column of 1 to your data and then you should pass your data to the statsmodels.api.

sklearn linear regression:

Now, look at how we apply the sklearn linear regression on a dataset available here.
We will use the datasets from the sklearn. You can access datasets available from sklearn, using sklearn.datasets. We will take the load_boston command to load the Boston data. I will not go details about what and how the data is collected, but if you want to explore the Boston data on your own, please follow this link to know more about the data. Now in the following blocks of codes, see how the linear regression from sklearn is implemented.

This next screenshot shows that how to import linear regression using LinearRegression from sklearn.linear_model, how to fit a model using existing data and also how to predict for new data using the predict attribute. I have also imported and included the use of the general accuracy check and feature importance check. For all sorts of accuracy metrics, one generally has to use sklearn.metrics library. In this specific case, as I discussed mean_squared_error to be already a good check for the accuracy or error rate of linear regression, I have imported mean_squared_error from sklearn.metrics and used it to check the accuracy of the linear regression. Mainly the values to be predicted are in 20-30 range, and we have got a mse of 21.84, which is around an error of 4.5-4.6 on the average; which is a mediocre level of prediction and a type of accuracy you can expect from linear regression on normal data. Also, we have imported the R squared score as it is one of the other significant markers of the accuracy of linear regression.
For the R-square score, one uses the R2-score function from the sklearn.metrics module. It is also as easy to use as the mean squared error.
One other noticeable point from programming nicety view is that how I have imported these functions with big names as small abbreviations. This eases up both writing time and usage over the code. Although this doesn't have any efficiency effect on the programming just to be clear.

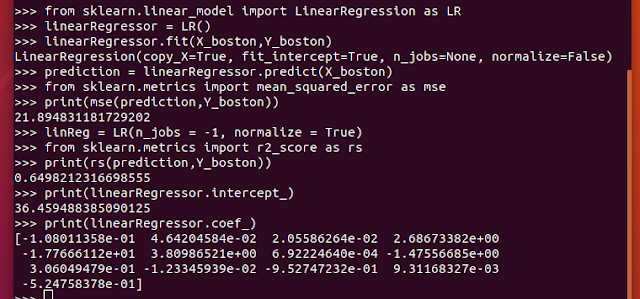
We have achieved a 64% Rsquare in the linear regression made in the following block; which is kind of a good explainability. There will always be project-specific requirement in your modeling though which will sometime become more important than just mse and r-square, but those are generally beyond statistical scope of linear regression and therefore no need to discuss in this blog.
Next lets see how we can use statsmodel package on the same data. We will just show the package use part as we already have the data loaded.

statsmodel linear regression:

references

For reading a simple yet beautiful example of linear regression, follow this blog by Ritchie ng which has a nice use of the linear model on a dataset and is readable and workable as it comes stepwise.