Introduction to PCA analysis
project and writing: shyambhu mukherjee, solanki kundu
Introduction:
PCA(principal component analysis) is one of the major mathematical techniques used regularly behind dimension reduction, feature reduction, and low dimensional visualizations. PCA is dependent on the idea of eigenvalue decomposition of symmetric matrices.
Summary of article:
In this article, we will start with basic concept of PCA and discuss the various ways to perform PCA visualizations and results. Then, once you are down with basics and usage, we will get into the linear algebra behind PCA; discuss why and how eigenvalues come into picture and how to practically use PCA, choose dimensions and all that. By the end of this article, you will be confident to use and explain PCA analysis. If you already use pca, still I guess this article will work as a great refresher for you.
PCAs are nothing but modified eigen-vectors:
In PCA, the main goal is to find out a lower dimensional representation of our data, while keeping as much as variance in the data as possible. For this, we try to find out basically new linear combinations of the features in the data, which are uncorrelated; as well as can present as much information as possible from the matrix. And with the magic of linear algebra[which we can prove too]; we know that eigenvectors of the covariance matrix represent these combinations.
So in short, principal component for your data are nothing but eigen vectors of the co-variance matrix multiplied with your feature matrix. It is as simple as that. And the good advantage of using a language like python is that, now without even knowing what are eigenvalues and eigenvectors; we can go forward and do PCA in our data.
How to do PCA in your data:
For the visualization and codes we will use pieces of this amazing notebook written by Solanki kundu. Some of the codes are taken from this reference. First things first, for doing pca, your data needs to be standardized. Standardizing means setting the feature mean to 0 and variance to 1. To do this, we will use StandardScaler() from sklearn.preprocessing. i.e.
In these two easy lines, your data is scaled. Now that the data is scaled; we will create a pca object and do the pca transformation. To this the following code works:
Now, we have fit and transformed the data into data_pca_ncomp; which is a numpy ndarray containing the two pca components made from the data. To easily access the components; we will turn it into a dataframe.
Now, in the notebook, we have used iris dataset and used the above codes to create the pca. Now we will plot these two pca; to see the 2d visualization of the dataset. Before that, we will attach the target file of different flower patterns to provide different colors in the visualization.
This is the exact code of plotting this data.
Now, let's see how this PCA looks:
If you don't understand the plot codes, please refer to the official plotting guide. Otherwise you will understand that we are simply creating fig and ax for the figure and axis of the plots; and adding the labels and titles to the axes, and then plotting using scatter plot. So the resultant picture is basically that scatter plot of the pca component 1 and pca component 2.
You can also check the explained variance to the whole variance ratio in pca using the following explained_variance_ratio attribute of the pca object.
array([0.72770452, 0.23030523])
Clearly, 95% of the variance is explained by the first two components; with respectively 72.7% and 23.03% achieved by the first and second components. So we just completed the basics of how to do PCA in your data. Do note that, we use numeric features only for doing PCA and not categorical features; as that doesn't make sense from the matrix concept. Now, in the next section, we will dive into the derivation of how eigenvectors become principal components and how PCA is therefore an efficient way to reduce dimension of data.
The theory behind PCA:
Now that we are going to read the hard part, I will be naive and assume that you don't know much of linear algebra and therefore start with linear algebra; explain what eigenvalues and eigenvectors are; and finally deduce how PCA's are eigen vectors from statistical calculations. So let's get started.
Linear algebra refresher:
For a matrix A, we define vectors as eigen vectors, which on multiplying with the matrix; does not change their direction. That translates to the fact that,
Av = kv where A is the matrix, v is the vector and k is the eigen value.
So clearly, eigenvectors, come with an associated eigen value. This eigen value is basically the measure of how much the vector gets shrinked or expanded by the matrix.
Consider the geometric aspect of this concept. The matrix multiplication; if you think from a geometric perspective; is actually nothing but creating a linear combination of a number of multiples of the vector. Which is again nothing but basically vector additions. So the fact that the matrix doesn't change the direction of the vector; but just expand or shrink its size in the n-dimensional linear space; is somehow representative of the fact that the eigen vector also is a representative of the matrix in one direction.
It is okay if you don't get the above paragraph now; but once we complete this section, you will understand the paragraph and its significance.
Now to find pca, we need to understand the mathematical definition of pca. Yeah I mean we know it is eigenvector multiplied by design matrix, but to derive that, we can't take that definition. So the more fundamental definition of pca is:
Principal components are orthogonal ( norm = 1) linear combination of the design matrix; which has the associated covariance matrix; with maximum variance reserved from the original covariance matrix.
So in mathematical words, let's consider the covariance matrix M.
Now, we consider a linear combination of the features coming from the data matrix ( or better called design matrix) as alpha1 as below:
Now, to maximize the variance means:
This needs again, well, a bit of a knowledge on lagrange multiplier. So basically to optimize multivariate functions based on constraints, we use lagrange multiplier. Under one constraint, consider a multivariate object variable maximization problem of n variable; i.e.
maximize f(x1,x2,...,xn) given g(x1,...xk) = 0
To resolve this problem from the constraint, we add another variable using the constraint and call this extra variable lagrange multiplier.
So this is how the problem is formulated. We just need to understand this much. And then from lagrange's theorem the following solution of the optimization problem follows:
So the solution then is nothing but the point at which the gradient of the modified problem becomes 0. You can think of it as basically an advanced version of differentiating a function and equaling it to zero to find maximum value.
So we will apply this in the matrix's variance optimization problem now. Confused? well the matrix's problem is again exactly such a n variable problem, with the constraint of the norm of pca being 1. So we therefore differentiate the reformulated version of the variance problem and then equal it to 0. That finally gives us the form of eigen vector. See the calculation below:
Now, as the derivation part is over, we reach our final conclusion which is that kth principal component is nothing but kth eigen vector of covariance matrix multiplied by the design matrix.
So this ends the mathematical derivation of the first principal component. Using induction and small amount of calculation, rest can be also proved. Although we used some fancy tool like lagrange multiplier, the core concept of the derivation was simple. We had a variance matrix to maximize; so we trickily derived it and got the maximum value.The geometric interpretation of this is as I was discussing related to eigen value. The matrix's variance is best reserved in the direction of eigen vectors as those are invariant of the matrix on multiplication.
Real project PCA application and elbow plot:
Now that you understand PCA, you probably do realize that it is much more than just visualization. For highly correlated data, which real noisy data often is, we always apply PCA to both reduce dimensions; and also to find orthogonal and thus uncorrelated features. Also, one more important point in doing practical PCA is to use a elbow approach in selecting number of components. I will shortly describe the elbow plot heuristic in pca.
PCA components have decreasing value of corresponding eigen values; and therefore reproduces diminishing percentage of the total variance of the design matrix. Therefore, we can plot the explained_variance percentages of each components and plot it. The plots generally look something like this below:
The elbow heuristic is that you choose the L or elbow looking point for optimal number of PCA components. Reason being after the sharp decrease, the more number of PCAs increase number of features; but the amount of variance increment becomes negligible. That's why we choose at the elbow point. In the above example we have attached a R-scree plot. Scree plot even points out the elbow point with a red line.Another simple approach of choosing pca component is just running cumulative sum on the explained_variance_ratio; and then thresholding it at a 95%, 99% or even at lower values like 75%. It is based on the amount of data you want to keep.
Conclusion:
In conclusion I will say that PCA is just a simple thing in a data scientist's day to day data modification processes. But in this article we went over the rigor of knowing what and how and whys of the pca; to reach that clarity about the tool we use everyday. Hope that it was a good read for you. I would like if you comment below your thoughts/criticisms; and also subscribe to my blog for more such contents.
Happy reading!
References:
(2) sebastian raschka: implementing pca step by step
(3) eigenvalues of symmetric matrices
(4) PCA,t-sne colab notebook created by Solanki kundu
(5) PCA mathematical derivation lecture notes
(6) Introduction to PCA(codes are partially taken from this blog)








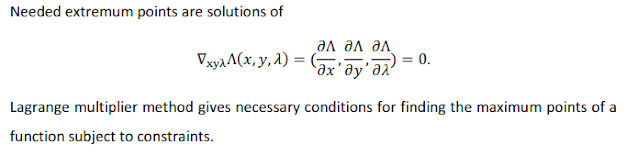



Comments
Post a Comment